Prime, Composite, Square, & Prime Factorization

When dealing with numbers, you can classify them into many different categories. In this post, we are going to look at the categories of prime, composite, and square. We will also take a look at prime factorization, which although is not a category for placing numbers, it will help you see the make up of the composite numbers.

Prime numbers are numbers that are only divisible by one and itself. Some examples of prime numbers are 2, 3, 5, 7, and 9. There are many more prime numbers, but that should give you a good look at what some are.

Composite numbers are numbers that are divisible by sets other than just one and itself. They are the exact opposite of a prime number. For example, 4 would be a composite number because it's factors are 1 times 4 and 2 times 2. As you can see, there is more than one way to divide this number to get a whole number. Other examples of composite numbers would be 6, 8, 9, and 10, and the list goes on and on.

Square numbers are numbers where a number is multiplied by itself to get the product. If you were to take the square root of a square number, you would get a solid whole number. For example, 4 would be a square number because it is the product of 2 times 2. Some other examples of square numbers would be 9, 16, 25, and 36. As you can see, square numbers are also classified as composite numbers, because they have more than one set of numbers that can be multiplied into and divided out of them.

Prime Factorization is a unique way to write out a number. There are no two numbers that have the same prime factorization. An example of a prime factorization we could look at would be for the number 48. We start by breaking 48 down into all the prime numbers that go into it. So if we start at the first prime (2), 48 divided by 2 is 24. Divide that answer by 2 again, and you get 12. You can divide that number by 2 as well and you would then have 6. You can divide that by 2 and your answer would be 3. So the prime factorization for the number 48 would be 2x2x2x2x3, or otherwise known as 2^4 (two to the fourth power) times 3. The prime factorization of a number shows the quantity of prime numbers you multiply together to get to the original number.

Divisibility Tests

There are some rules that you can use to quickly check if a number is divisible by any number from two to twelve. We can call these divisibility tests. There are some that are not that useful, such as seven and eleven. For those particular numbers, you will probably find it just as simple to figure it out by just simply doing the division. But for the rest of the numbers, there are some very helpful hints.

Divisibility by two: If the last digit of the number is divisible by two, then the whole number is divisible by two.

Divisibility by three: Take the sum of all the digits of a number, and if the sum is divisible by three, then the whole number is divisible by three.

Divisibility by four: When you look at the last two digits of a number, if that two-digit number is divisible by four, then the whole number is divisible by four. You would only have to look at the last two digits of a number because four is divided equally into one-hundred, so therefore you already know that you only have to focus on the last two digits.

Divisibility by five: If the last digit is a zero or five, then the whole number is divisible by five.

Divisibility by six: Because six is the result of two times three, if the number is divisible by two and by three, then the whole number is divisible by six.

Divisibility by eight: When you look at the last three digits off a number, if that three-digit number is divisible by eight, then the whole number is divisible by eight. You would only have to look at the last three digits of a number because eight is divided equally into one-thousand, so therefore you already know that you only have to focus on the last three digits.

Divisibility by nine: Take the sum of all the digits of the number, and if the sum is divisible by nine, then the whole number is divisible by nine.

Divisibility by ten: If the number ends in a zero, then the number is divisible by ten.

Divisibility by twelve: Because twelve is the result of three times four, if the number is divisible by three and by four, then the whole number is divisible by twelve.

These simple rules, if remember, will help you tremendously when dealing with larger numbers. It will help you break those numbers down into easier, and more manageable numbers to work with.

Base 12

The base 12 number system is more like the base 5 number system versus the base 10 number system, there are just more numbers involved (number values). This number system uses 12 different values; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, T (10), and E (11). The reason why 12 is not used is because once you get to that value, you move to the next placement value. The placements are one's, twelves, one-hundred forty four, and so on. The placements are also known as the powers of 12. For some background information on this system click here.

The number 236 base twelve is actually the number 330 in base ten. You get this answer by multiplying 2 by 144, adding that to 3 times 12, and then finally adding that to 6 times 1. Lets try another one... the number 5T1 base twelve would be 841 base ten. Remember, multiply 5 by 144, add that to 10 times 12, and then add 1 times 1.

Base 10

The Base 10 number system is probably the one most of us use and love. It is the basic system used for counting and writing out numbers we use on a daily basis. It has ten digits; 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The placements are ones, tens, hundreds, thousands, and so on. We use this number when we talk about population, money, most American math, and almost anything else you can think of. It is also known as the decimal system. To get a little history/background on this number system click here.

I personally view this as the easiest of the number systems, although that is probably because it is what I grew up with. We use the base 10 number system daily in our lives, and it comes so naturally to us, we don't even really have to think about it. This system is used the most out of all of them throughout the world.

Base 5

The base 5 number system is somewhat difficult to understand. The placement of the numbers goes ones, fives, twenty-five, and so on. They are also known as the powers of five. You write the number out by putting the number of fives that go in that spot, never using any other numbers but 0, 1, 2, 3, and 4. The reason you never use 5 is because once you get to that value, you move it to the next placement. For example, the number 421 base five is really the number 115. This is because the 4 is in the 25's placement, the 2 is in the 5's placement, and the 1 is in the 1's placement. To get 115, you multiply 25 by 4, add that to 5 times 2, and then add that to 1 times 1.

This number system is somewhat confusing to a lot of people at first. It takes a little thinking to learn it and to understand it. Not a lot of places in the world use this method. For a little bit of background or history of the base five number system click here. Like the link tells us, the base five system can also be thought of as the hand based number system. It is used more as a grouping system.

Different Culture's Number Systems

Different culture's have very different number systems. In my college math class we learned about 3 different culture's. We learned about the Egyptian, Babylonian, and Mayan number systems. Instead of the natural numbers that we use in our society, they use symbols to represent their numbers.

The Egyptians use seven different symbols for their numbers, the stick, heel bone/yolk, coiled rope, lotus flower, pointing finger, tadpole, and the astonished man. (For some help with these symbols click here.) Each symbol (starting with the stick and ending with the astonished man) represents different values of ten.

The Babylonians use two different symbols for their numbers, the 'T' and the wedge. (For some help with these symbols click here.) The "T" stands for both one and sixty, the wedge stands for tens.

The Mayans use thr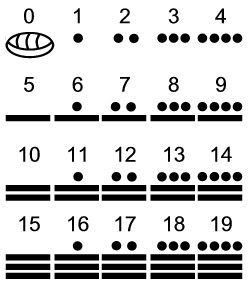ee different symbols for their numbers, the line, dot, and all seeing eye. (For some help with these symbols click here.) The all seeing eye stands for both zero and 20, the dots stand for one, and the line stands for five.